理查德-费曼如何求复杂函数的导数的。非常聪明的求导技巧

理查德-费曼（Richard Feynman）是美国理论物理学家，与美国物理学家朱利安-施翁格（Julian Schwinger）和日本物理学家友永信一郎（Shinichiro Tomonaga）配合得到1965年诺贝尔物理学奖。他是天下上最有名的科学家之一。在1999年英国《物理天下》杂志对环球130位顶尖物理学家的平易近意查询拜访中，他被评为有史以来十年夜最巨大的物理学家之一。

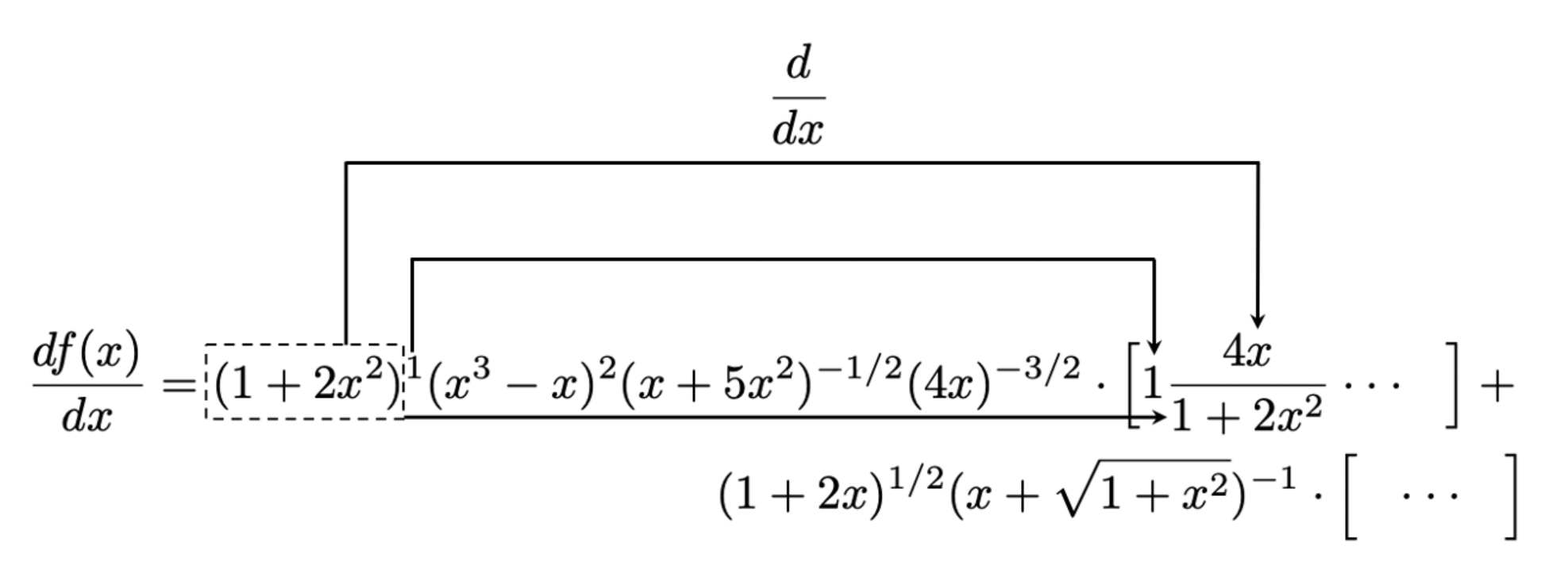
图1，1965年得到诺贝尔奖后，费曼在欧洲核子研讨中心的研究会上谈话

费曼对物理学做出了一些根基性的进献。这些包含量子力学的路径积分公式，量子电动力学理论（描写亚原子粒子行动的图形表现，有名的费曼图），以及液氦的超流体性的理论解释。他也是量子计算范畴的前驱，引入了纳米技术的观点，以及其他很多器械。费曼也是一位有名的物理学科普者。

图2，费曼图的一个例子。在这里，一个电子（e⁻）和一个正电子（e⁺）泯没，发生一个光子γ。光子就酿成了一个夸克-反夸克对，之后，反夸克辐射出一个胶子g。

费曼曾经如许描写他对科学的见地：

假如你愿望科学能给出关于我们是什么的所有谜底，我们要去哪里，宇宙的意义是什么……你很容易破灭，然后探求一个神秘的谜底……我们正在摸索，试图尽可能多地相识这个天下。人们会问我，你在探求最终物理定律吗。不，我没有，我只是想多相识一下这个天下。假如事实证实有一个最终轨则可以解释统统，那就天真烂漫吧，这将是一个异常好的发现。

假如事实证实它像洋葱，稀有百万层，那么它便是如许的。但不管成果若何，这都是天然的，她会酿成她本身的样子。是以，我们不该该预先决议我们将要发现的是什么，除非测验考试去发现更多。假如你以为你能获得一些深邃的哲学问题的谜底，那你可能错了——你可能无法经由过程更多地相识天然的特征来获得这个特定问题的谜底。但我不这么看，我对科学的兴致是要更多地相识这个天下，我发现的越多越好。——理查德-费曼

费曼微积分的条记本

20世纪30年月初，费曼还在法洛克威高中念书时，依据一本名为《适用人士微积分》（Calculus for the Practical Man）的书，他整顿了一套手写条记。在谁人时刻，对一个高中生来说，有一个微积分先生是很不寻常的。费曼的条记与那本书慎密相连，他从头至尾逐字逐句地浏览那本书。

正如《今日物理》所指出的那样，“费曼的微积分条记阐明了这位有名物理学家的决议性特质之一，他永不满意的好奇心……当他发现一门令他感兴致的学科时，他不会坐等适宜的先生呈现，他必定会本身掌握它。”

图3，费曼的条记本。

本部门紧随着费曼、莱顿（Leighton）和桑兹（ Sands）所著的书，以下将其称为FLR。在这本书中，费曼描写了一种快速计算繁杂的多乘积函数的导数的聪慧办法。

简单函数的导数

要懂得费曼办法，我们只必要知道以下类型的导数：

方程1，费曼算法中使用的简单导数的例子。

更繁杂函数的导数

这里将用到的FRS中的例子是：

方程2，待微分函数。

追随费曼，第一步是反复f（x）中的两项，每项乘以一个尚未肯定的表达式，如下所示：

方程3，微分f（x）的第一步。

这两项都包括一个分子因式的乘积和另一个分母因式的乘积。为便利起见，我们可以将表达式写成：

方程4，用更便利的方式写方程3。

括号内的表达式是函数的和。为了获得这些和的每一项，我们利用下面的3步算法。例如，斟酌第一个因式，即（1+2x²）这三个步调是：

这个因式酿成了两个括号中第一项的分母这个因式的指数，也便是1，酿成了第一个括号内第一项的前因式这个因式的导数酿成了第一个括号内第一项的分子

下面的原理图使算法加倍详细：

方程5，将算法利用到f（x）第一项的第一个因式上。

如今，将算法利用到f（x）第一项的第二个因式上：

方程6，将算法利用于第一项的第二个因式。

将该算法利用于所有项，获得f（x）的导数，即：

方程7，将算法利用到整个表达式，获得终极成果。

算法的广泛化

方程2是两项的和，每一项的情势如下：

方程8，方程2中两项各一项的情势。

方程8的导数的一样平常情势为：

方程9，对方程7的推广。

想相识更多出色内容，快来存眷老乱说科学